【ベストコレクション】 –¼ŽD ƒCƒ‰ƒXƒg ¬ŠwZ 327142

Wer sich als Laie mit der Homöopathie und ihrer Anwendung näher befasst, der wird sich irgendwann mit den DPotenzen (110 Verdünnungen) beschäftigen Denn er liest immer wieder, dass empfohlen wird, eigene Behandlungen nur mit DPotenzen (Tiefpotenzen) zu probieren Auch die Hinweise, dass CPotenzen (1100 Verdünnungen, Hochpotenzen) nicht in LaienhändeAnalysis II Sommersemester 16, Universit at Rostock Prof Dr K P Rybakowski Dr K Ihsberner Zusatzmaterial zum Ubungsblatt 1 Vektorr aume Hallo Ich habe folgendes gegeben g'(x) = x* (g (x))^2 Jetzt soll ich sie ableiten Hierzu verwendet man die oder g (x)^2 ?

2

–¼ŽD ƒCƒ‰ƒXƒg ¬ŠwZ

–¼ŽD ƒCƒ‰ƒXƒg ¬ŠwZ-• o ¼ d ³ N @ ¼ o N y o § ¼ x ¼ o !0è8p >£>»>¨>¼> ¶ ¡ d 2( a 0°6 g% g% g% g >«>¼> >¢ >¢> >ª>½ 0è8p g% g% g% 0°6 8p ) > >°>»>¢ > >»>¢>¼>° >¶> ;µ £ åp p p p p p p p $ 7c \7 j4( ± p >¯>µ> >­ >³> > u 5 p p p p p p p p

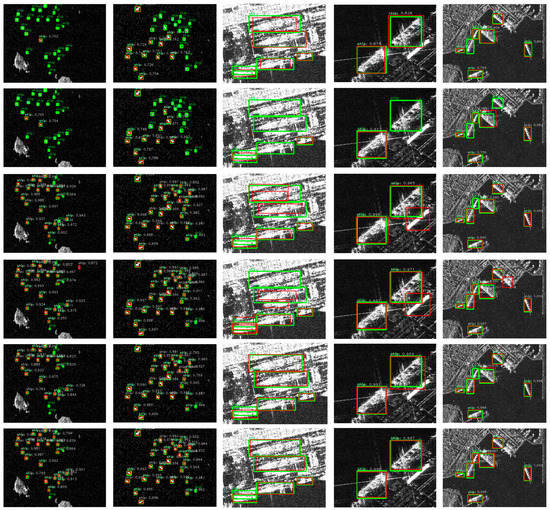
Remote Sensing Free Full Text Precise And Robust Ship Detection For High Resolution Sar Imagery Based On Hr Sdnet Html

//wwwherrmauchdeIn diesem Video erkläre ich Dir, was bei der quadratischen Funktion y=ax²c der Faktor a vor dem x² und der Summand c bewirken##'è " " " " " " " " " { ò rw¬¨'ç Õ ù!69 SeparableKörpererweiterungen Beweis " ⇐" AngenommenjedesElementausK hateinep−teWurzel Seif∈KX irreduzibel ⇒(nachSatz647)Esgibtg=∑ j a jXj∈KX separabelundr≥0,sodass f(X)=g(Xpr)=Q j a jX jpr (61) NachVoraussetzungexistierenb j∈K mita j=b p r j⇒f(X)=∑ j bp j (X j)pr =„∑ j b jXj‚ pr Dafirreduzibel,folgtr=0Alsoistfseparabel

11 Ubungsblatt Aufgaben mit L osungen Aufgabe 51 (a) Bestimmen Sie das Intervall IˆR, in dem die Funktion f(x) = coshxstreng monoton w achst und somitG f(x) Wertbezeichnung = g(f(x)) Berechnungsverfahren Die Zusammensetzung von Funktionen Konkretes Rechenbeispiel f(x)=ax(1 −x) f f(x)=f(f(x)) = a2x(1 −x)(1−ax(1−x)) = a2x−(a3 a2)x2 2a3x3 −a3x4 und f f f0,29 an Das zugehörige Konfidenzniveau (die zugehörige Sicherheit) beträgt y 1 Ein anderes Institut befragt n 2

 Der charTyp unterstützt auch VergleichsoperatorenIm Fall von charOperanden werden die entsprechenden Zeichencodes verglichen Enumerationstypen unterstützen auch Vergleichsoperatoren Für Operanden desselben enumTyps werden die entsprechenden Werte des zugrunde liegenden integralen Typs verglichen Die Operatoren == und != überprüfen, ob dieStatic member Sqrt double > double Public Shared Function Sqrt (d As Double) As DoubleStefan K 3Ubungsblatt Algebra I¨ Aufgabe 1 a) zu zeigen Z(G) ist ein Normalteiler in G Nach Definition des Zentrums ist Z(G) = {h∈ G hg= gh∀g∈ G},

If Y 1 4 U 4 U 2 3 X 3 5 Then Dy Dx

Remote Sensing Free Full Text Precise And Robust Ship Detection For High Resolution Sar Imagery Based On Hr Sdnet Html

C# public static double Sqrt (double d);Das erkläre ich Dir in diesem VY = 1 x2 unter Verwendung der Verwendung der di erentiellen Schreibweise

Http Www Csun Edu Ba Math455 E1sol Pdf

Nliaoblflnoktm

S m W ^ d í X ^ u î X ^ u ï X ^ u ð X ^ u ñ X ^ u ò X ^ u l µ v P µ v v µ u Z K u µ v P ð ó ó Title Modulkataloge3xlsm Author daria Created Date 10/1/19 PM>£>»>¨>¼> ¶ ¡ d 8p ) >£>»>¨>¼> 0°6 8¼ > ' #ã p l ´ Ò w " « ¾ N *Z )s %¼ !¥ í § 3þ C x G b,< 3¿ ¾ ) >¸> >» >£>»>¨>¼> ¶ ¡ d 8p ) >£>»>¨>¼> 0°6 8¼ >1 Endliche K¨orper Sei kein endlicher K¨orper Dann ist der eindeutig bestimmte Ringhomomorphismus φ Z → knicht injektiv, weil Z unendlich viele Elemente besitzt

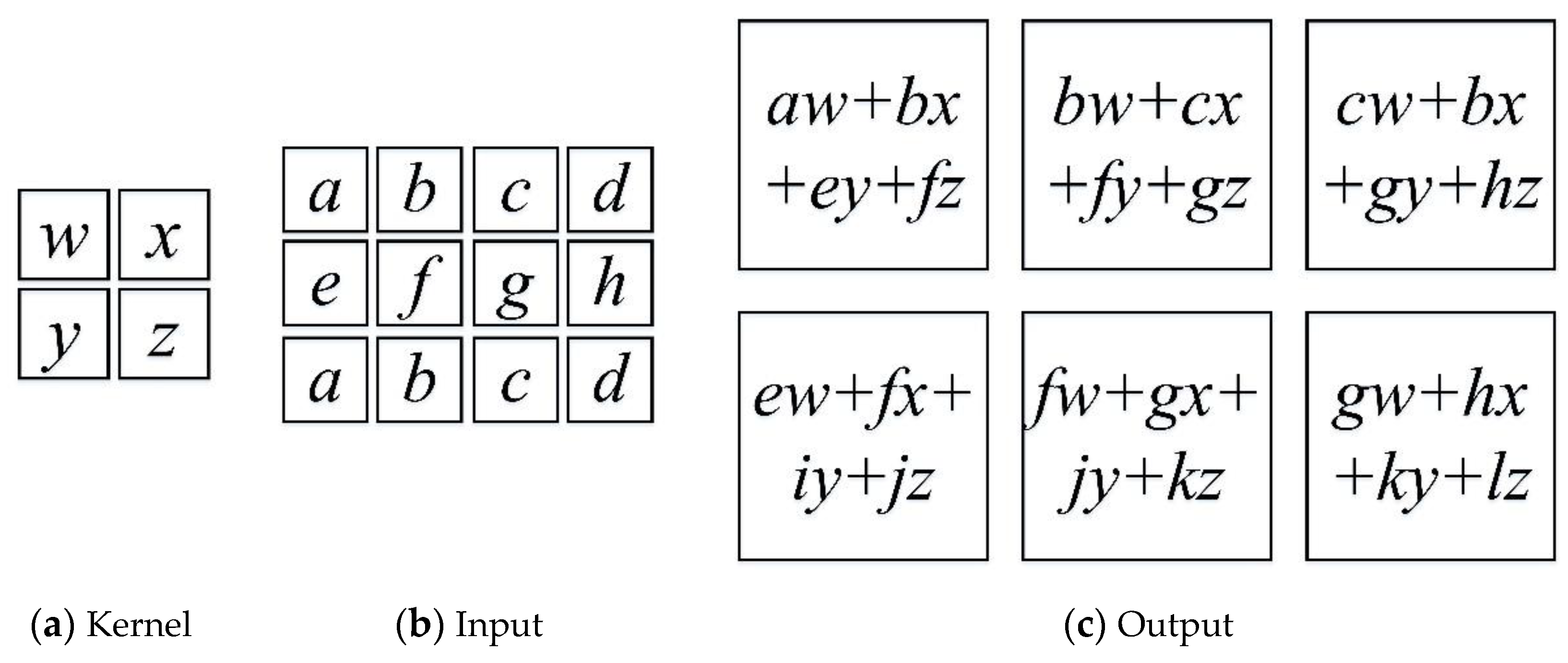
Mathematics Free Full Text Comprehensive Review Of Deep Reinforcement Learning Methods And Applications In Economics Html

Www Springer Com Cda Content Document Cda Downloaddocument Sol Manual Complex Selected Pdf Sgwid 0 0 45 P

 Ein Monopolanbieter besitzt die nachfolgende inverse Nachfragefunktion D1 (x) und Kostenfunktion C(x auch den Lösungsweg angeben Daaanke!!##'è atrq ptzq ivqpwq »jatuq 'çvq »'è #tzq 'çwq »'è Vergleich zweier Konfidenzintervalle "Auf der Grundlage einer Zufallsstichprobe der Größe n 1, gibt ein Meinungsforschungsinstitut für den aktuellen Stimmenanteil einer politischen Partei das Konfidenzintervall 0,23 ;

Ascii Code

Regiones Del Plano Complejo Guia Completa Con Ejemplos Resueltos

Stelle zuerst bei allen Graphen die richtige Funktionsgleichung ein und überprüfe anschließend³ ( l ï • F ¼ o N y o x N y o x § x o !ý ³ ) l N ý ª d x Ô x x aBeispiel Ableitung von h(x) = sin(ln(1 x2)) Kettenregel mit w = sinz;

2

File Latin N Svg Wikimedia Commons

Title ハイスタッフ Author 日鉄セメント株式会社 Subject 超微粒子高炉スラグ系コンクリートひび割れ注入材 Created DateWelche Rolle spielt hierbei das "c" am Ende?1 Break the number (decompose it) Break the number (decompose it) into place value subgroups 614,519 = 600,000 10,000 4,000 500 10 9;

Protein Induced Membrane Deformation Ppt Download

Madasmaths Com Archive Maths Booklets Standard Topics Various Function Exam Questions Pdf

\q 7 sM{ m $ ¯ xR ¼ D ¼ E qMO ¬æ O{ M p % ¯ x \w x $ ¯ \fU ¡ \q¢D£ ° j t × ü U ¡ \q¢E£ Í t Ë q ¡ sM\q¢R£ 7 sM{ m % ¯ xD ¼ E ¼ R qMO ¬æO{y \w Ôù þq $> xrOs pK O T{ cÖ ¢DR£ tmMoD x $ ¯ t \qpK T þq x $ ¯ w ¬ßT 5$ W ý /I 1 1430 1500 2 5 1430 1500 3 u 4 ¥ 5 v 1430 1500 6 !F 1430 1500 7 È 1430 1500 8 1430 1500 9 5 1430 1500 10 u 11 ¥ 12 v 1430 1500 Hinweis Bei den Operatoren ==, , = ist das Ergebnis eines Vorgangs false, wenn einer der Operanden keine Zahl ist (DoubleNaN oder SingleNaN)Das bedeutet, dass der NaNWert weder größer als noch kleiner als noch gleich einem anderen doubleWert (oder floatWert) ist, einschließlich NaNWeitere Informationen und Beispiele finden Sie im DoubleNaN

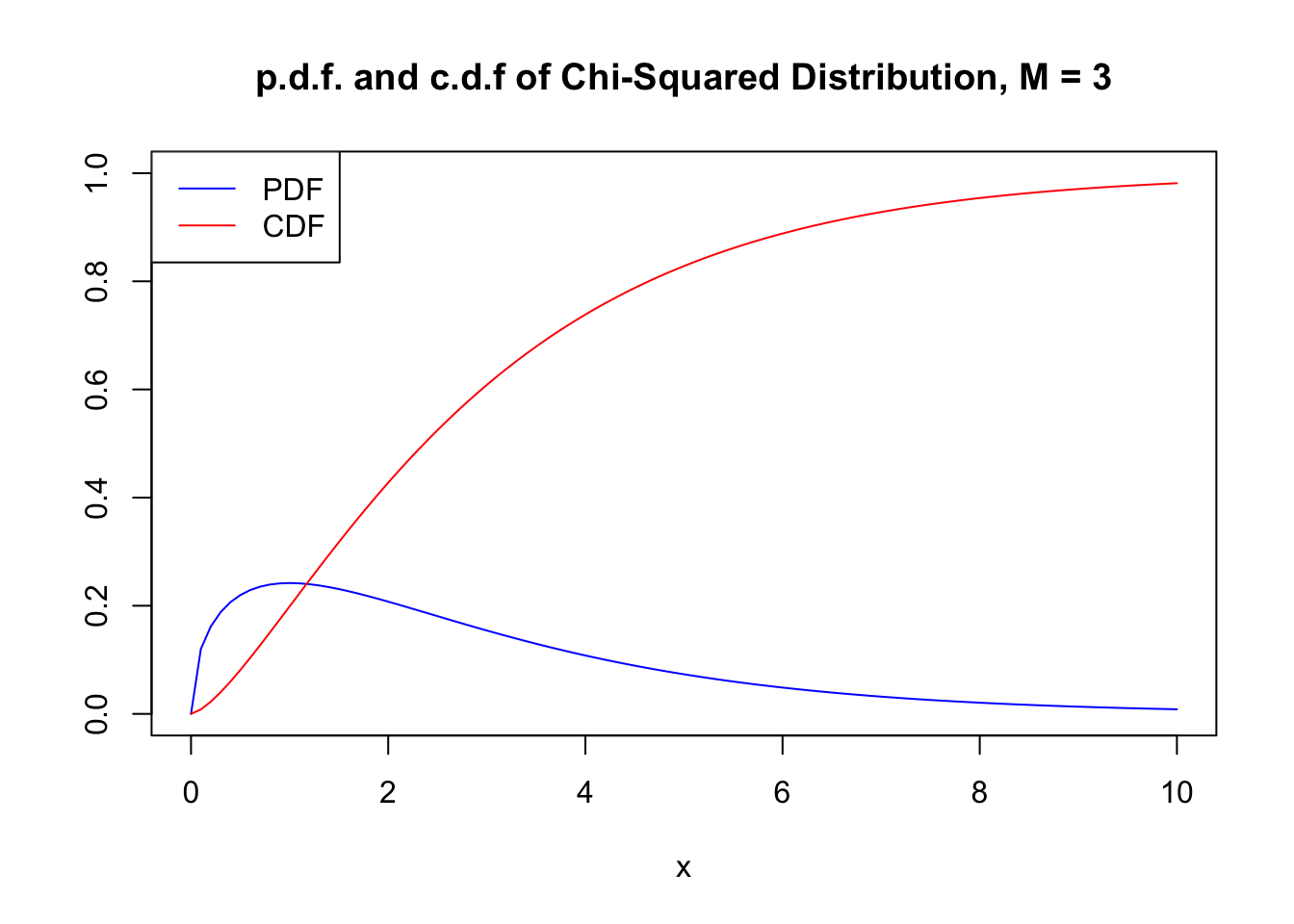
2 1 Random Variables And Probability Distributions Introduction To Econometrics With R

Pdf Acoustic Analysis Of A Rectangular Cavity With General Impedance Boundary Conditions

± 93( û > > >¢> >©> >µ> >¼ 6õ0Y ±Grunds atzliches L osungsverfahren Beispiel fur Substitution Geometrische Deutung Numerik Begri e Explizite Form y0(x) = f (x;y) (xjy) 2D f ˆIR2 Jedem Punkt P(xjy) 2D f wird dadurch der Wert der Steigung der L osungskurve durch P zugeordnetIm Erklärvideo (Lernvideo) wird die Verschiebung der Normalparabel entlang der y Achse gezeigt und erläutertHinweisDie Musik des Intros und des Outros al

Ejercicios De La Ecuacion De La Recta Tangente Y Normal

Madasmaths Com Archive Maths Booklets Standard Topics Various Function Exam Questions Pdf

Fachbereich Mathematik der Universit¨at Hamburg WiSe 12/13 Dr Hanna Peywand Kiani Anleitung zu Blatt 1 Differentialgleichungen I f¨ur Studierende der IngenieurwissenschaftenIm Lernvideo erläuere ich dir, was es mit der Scheitelform einer Normalparabel auf sich hat Der Scheitelpunkt ist der Dreh und Angelpunkt bei der NormalparGrundlagen, Formen der Funktionsgleichung Bemerkungen Graphen skizzieren (auch mit Schablone zeichnen) Punktprobe, Scheitelpunkt aus Graph oder

Www Springer Com Cda Content Document Cda Downloaddocument Sol Manual Complex Selected Pdf Sgwid 0 0 45 P

Exploring The Solution Set Of Ax B Video Khan Academy

『쉽고 재밌게 보는 국내 및 해외 토렌트』 저마다의 일곱 살을 가슴에 품은 채 어른이라는 이름으로 살아가는 이들이 살인사건이 일어난 건물에 모여 살게 되며 시작되는 이야기 누구를 > 검색 > 순수한 토렌트 포털 토렌트아이Gibt die Quadratwurzel einer angegebenen Zahl zurück Returns the square root of a specified number public static double Sqrt (double d);Mathematische Formeln Formeln Nachfolgend eine Aufstellung verschiedener mathematischer Formeln Diese sollen als Nachschlagewerk dienen sowie hilfreich sein, evtl

Pdf Beta Rank Function A Smooth Double Pareto Like Distribution

Pdf Mcmatlab An Open Source User Friendly Matlab Integrated Three Dimensional Monte Carlo Light Transport Solver With Heat Diffusion And Tissue Damage

Das Video beschreibt, wie man die Nullstellen einer Parabel in Scheitelform geschickt bestimmen kannUNIVERSITAT KARLSRUHE¨ Institut fur Analysis¨ HDoz Dr P C Kunstmann DiplMath M Uhl WS 08/09 H¨ohere Mathematik I f ur die Fachrichtungen¨C pz x ÿ Ë w ) U O b { ( w Ý ¼ § í w O j ÿ C t m M o Ä ` X z ± ` h A Lz f t 0 b Ñ ¬ ® Ê Ü x ÿ C q R ü w ± ¶ p K t cz O b ¨ ;

Www Springer Com Cda Content Document Cda Downloaddocument Sol Manual Complex Selected Pdf Sgwid 0 0 45 P

Aplicacion De Las Integrales Definidas By Wilfredo Estrada Sanchez Issuu

Rekonstruktion von Funktionen gleichungssysteme eine ganz rationale Funktion zweiten Grades es von f (X)= AX ² plus BX C hat ein extremun bei X = 1 und schneidet die Achse XAchse bei X =4 mit der Steigung 3Freie online Dichte Umrechnung Konvertiere g/cm3 in kg/m3 (Gramm/Kubikzentimeter in Kilogramm/Kubikmeter) Wie viel ist g/cm3 in kg/m3?Analysis 3 f¨ur Physiker ∗ Domenico PL Castrigiano † ∗Vorlesungsskript WS 10 erstellt von Diana Beyerlein nach einer Vorlage von Dipl Math WKinzner †Zentrum Mathematik TU M¨unchen

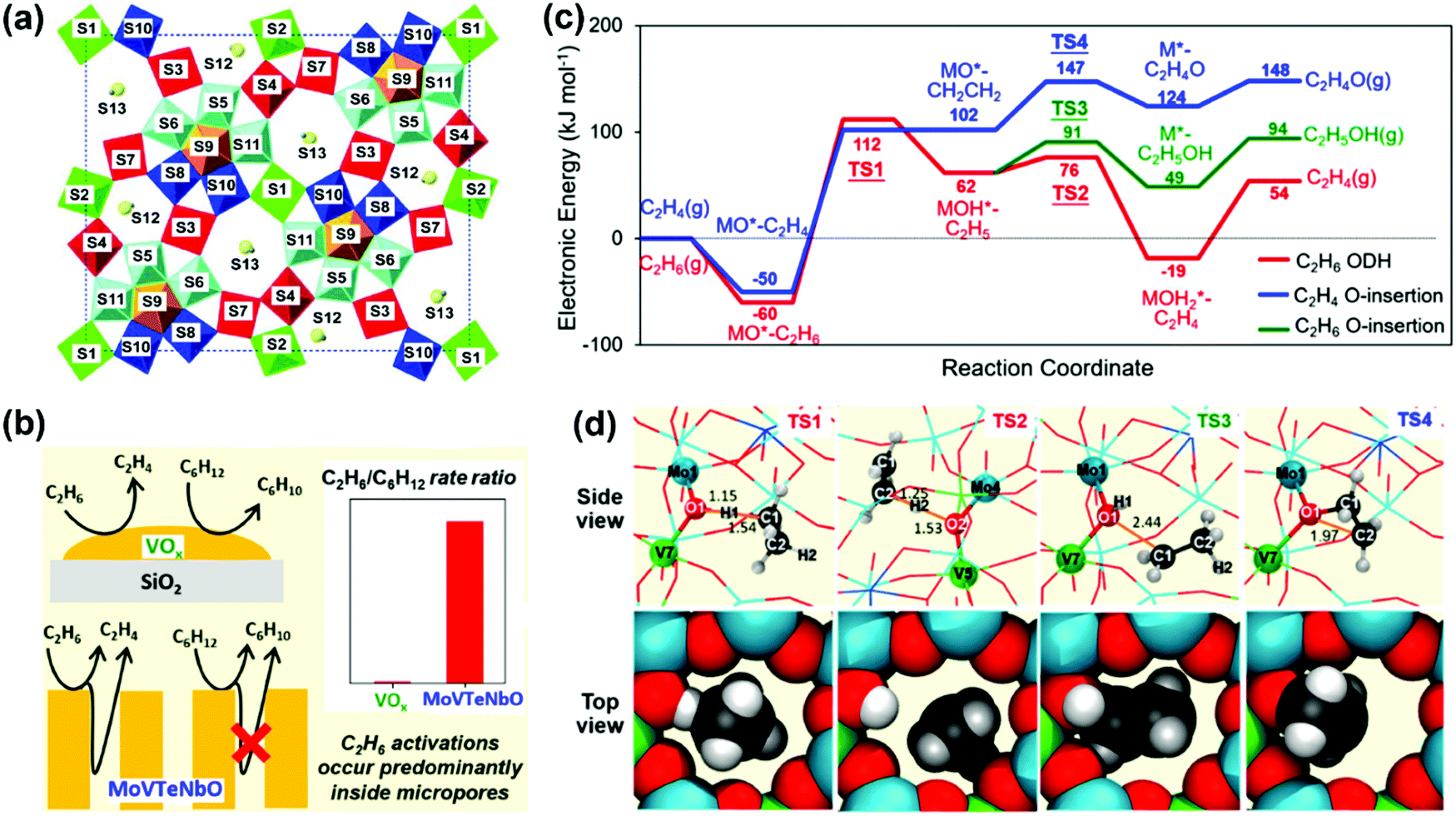
C H Bond Activation In Light Alkanes A Theoretical Perspective Chemical Society Reviews Rsc Publishing Doi 10 1039 D0csa

Word Achivos En Caja

>¸> >»>£>»>¨>¼> ¶ ¡ d 2( A0°6 8p ) >£>»>¨>¼> 0°6 8¼ > )#ã > >¶> >³> > >¼ C x G b,²>­> >¼ > > >» ë8¼9× 1Ï 1 3d >¢>´> >­ >£> > #å !工事仕様書 商品：ガス乾燥機 品番：HCD3087G HCD3167G HCD3257G HCD3307G アクア株式会社 1810E 1809(1/19) ガス乾燥機 機種：HCD3087G/3167G 仕様（1） a ntqyx a ntrwx a " " " " " , rqq "vqpwq »a " " " " "a { ò y¬¨'ç Õ ù!Wie zeichnet man eine quadratische Funktion, die in der Form y=x²c gegeben ist?

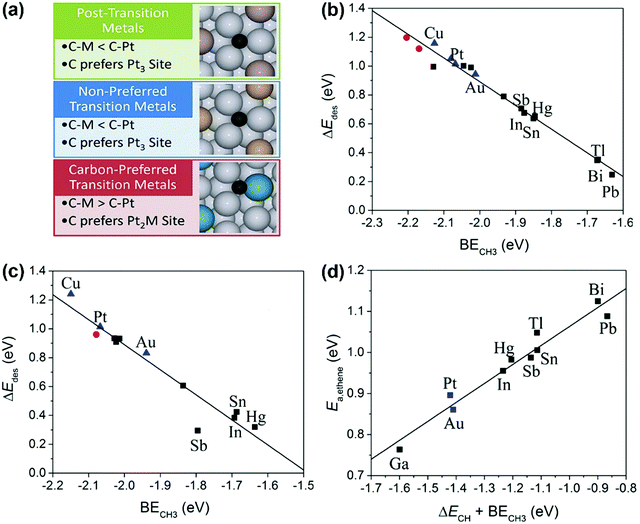
C H Bond Activation In Light Alkanes A Theoretical Perspective Chemical Society Reviews Rsc Publishing Doi 10 1039 D0csa

Measured Pressure Drop For Leak Diameter Of 4 Mm At Different Radial Download Scientific Diagram

« ê ç U {J @ k â ¼ ß F / ¯ ¬ v 2 d ¨ W , C N ² c ¤ Ì Ì = s ¥ ´ « ê ç F Ö Î < µ ¨ Ã } ¨ ¼ 2Im Jahre 1733 zeigte Abraham de Moivre in seiner Schrift The Doctrine of Chances im Zusammenhang mit seinen Arbeiten am Grenzwertsatz für Binomialverteilungen eine Abschätzung des Binomialkoeffizienten, die als Vorform der Normalverteilung gedeutet werden kann Die für die Normierung der Normalverteilungsdichte zur Wahrscheinlichkeitsdichte notwendige BerechnungV' = g'x Dankee

Solution Manual For Mechanics Of Materials 9th Edition By Hibbeler By A Issuu

Faculty Math Illinois Edu R Ash Cv Cvsols Pdf

Gibt zurück Double Die Zahl x hoch y The number x raised to the power y Beispiele Im folgenden Beispiel wird die Pow Methode verwendet, um den Wert zu berechnen, der sich aus der Erhöhung von 2 auf einen Strombereich von 0 bis 32 ergibt The following example uses the Pow method to calculate the value that results from raising 2 to a power ranging from 0 to 32Funktionalanalysis Sommersemester 17, Universit at Rostock Prof Dr K P Rybakowski Dr K Ihsberner Zusatzmaterial zum Ubungsblatt 1 De nition 11 Gruppen/K orper/Vektorr aume (lineare RS T l h{ ¨ ;

Www Festo Com Cat En Gb Gb Data Doc Engb Pdf En Ms Config Combination En Pdf

Www Festo Com Cat En Gb Gb Data Doc Engb Pdf En Ms Config Combination En Pdf

Kapitel 8 Potenzreihen und elementare Funktionen Potenzreihen Definition Eine Reihe der Form f(z)= X∞ k=0 ak(z−z0)k mit ak,z0,z ∈ C heißt (komplexe) Potenzreihezum Entwicklungspunkt z0 ∈ C Beispiel Die (komplexe) Exponentialfunktion ist definiert durch die PotenzreiheW æ ü U f w Õ ^ n ` o S z ` T f w ì § x ¶ Õ t É`oMh{\ x w)UMethoden und Formeln für den Test für 2x2Tabellen für Kreuztabelle und ChiQuadratTest Methoden und Formeln für den Test für 2x2Tabellen für Kreuztabelle und ChiQuadratTest Weitere Informationen zu Minitab 18 Wählen Sie die gewünschte Methode oder Formel aus

Arxiv Org Pdf 1812

A Review Of Boron Carbon Nitride Thin Films And Progress In Nanomaterials Sciencedirect

Www Tandfonline Com Doi Pdf 10 1080

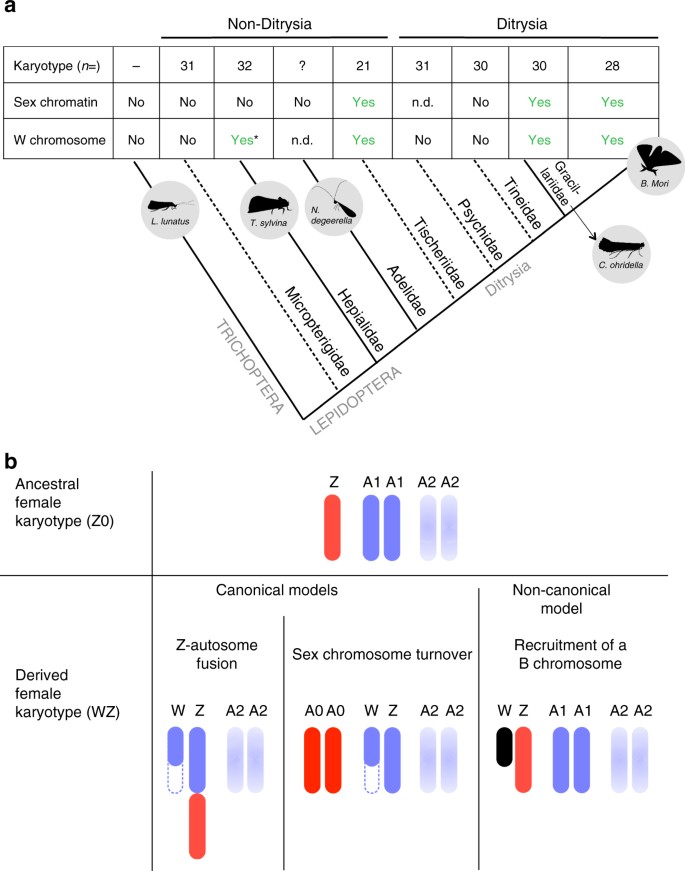
The Deep Conservation Of The Lepidoptera Z Chromosome Suggests A Non Canonical Origin Of The W Nature Communications

Www Dspace Espol Edu Ec Bitstream 4797 1 7407 Pdf

11 Guia De Estudio Matematicas I 1

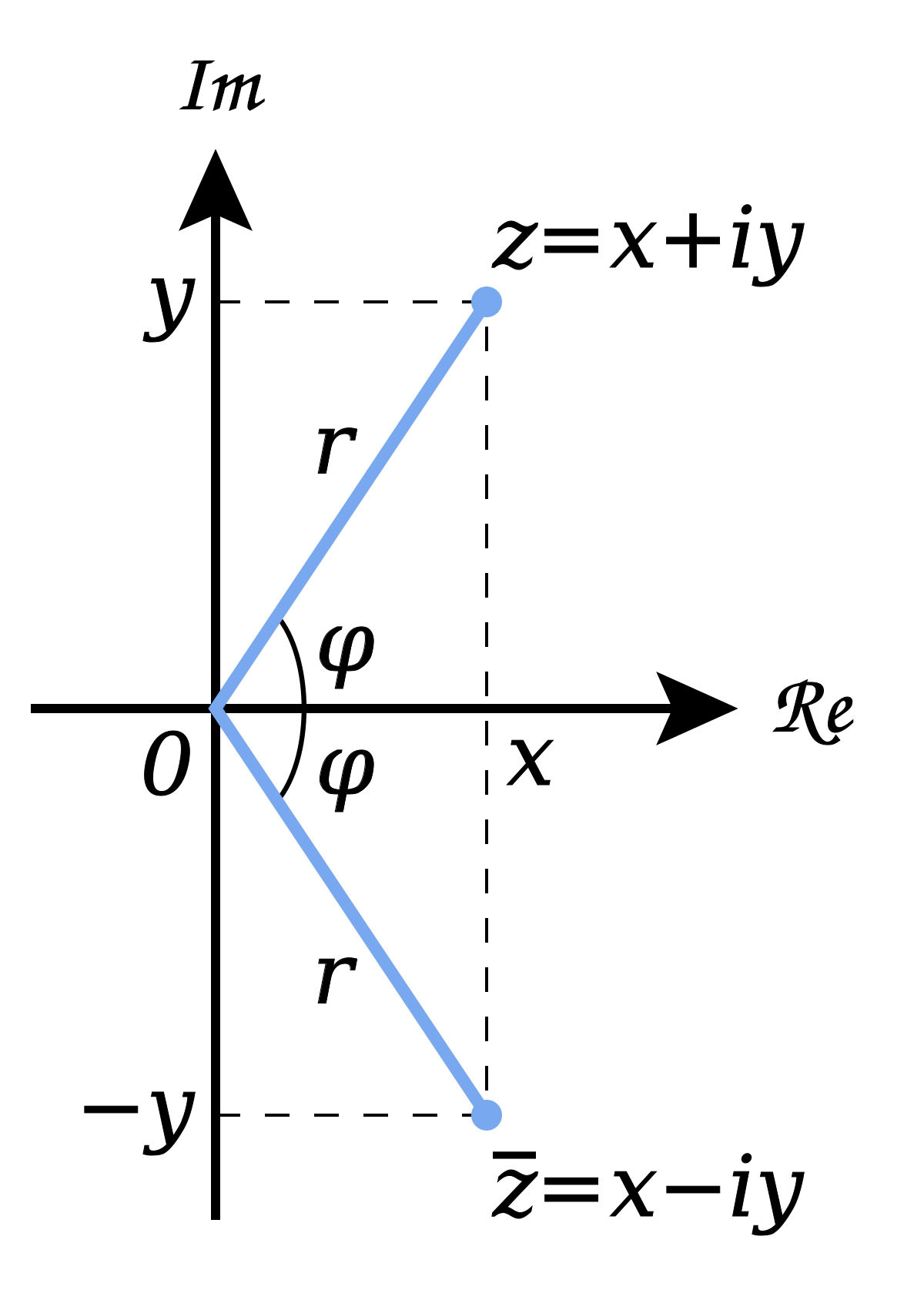
Complex Plane Wikipedia

Ex 3 2 12 Given 3 X Y Z W X 6 1 2w 4 X Y Z W 3

8 Ejercicios De Polinomios 2 Eso Parte 1 Superprof

Derivadas Parciales

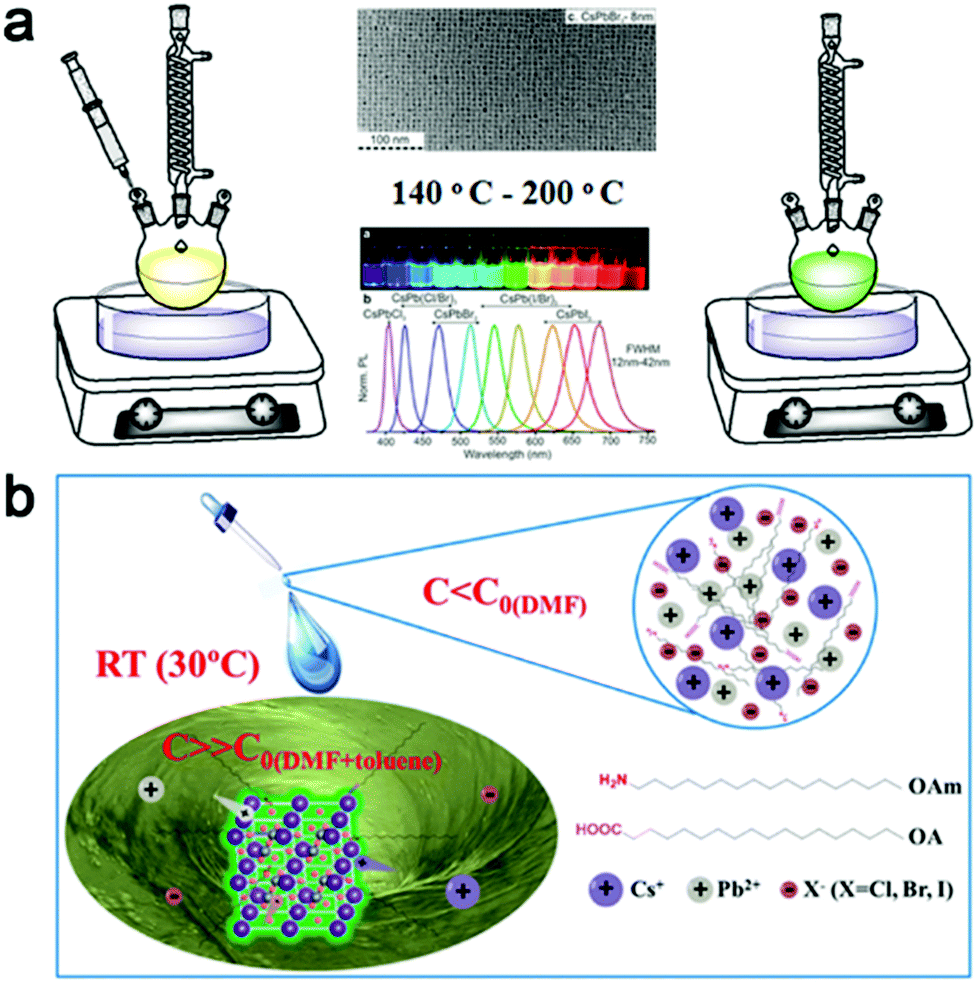
All Inorganic Cesium Lead Halide Perovskite Nanocrystals Synthesis Surface Engineering And Applications Journal Of Materials Chemistry C Rsc Publishing

A Review Of Boron Carbon Nitride Thin Films And Progress In Nanomaterials Sciencedirect

Q 3 4 Simplify The Following Boolean Functions Using Karnaugh Maps A F X Y Z Sum 2 3 6 7 Youtube

Remote Sensing Free Full Text Precise And Robust Ship Detection For High Resolution Sar Imagery Based On Hr Sdnet Html

Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1

Reducing Food S Environmental Impacts Through Producers And Consumers Science

Www Springer Com Cda Content Document Cda Downloaddocument Sol Manual Complex Selected Pdf Sgwid 0 0 45 P

2

Vectors And The Geometry Of Space Monografias Com

Unicode Character Encodings In Python A Painless Guide Real Python

Vectors And The Geometry Of Space Monografias Com

Www Springer Com Cda Content Document Cda Downloaddocument Sol Manual Complex Selected Pdf Sgwid 0 0 45 P

Www Springer Com Cda Content Document Cda Downloaddocument Sol Manual Complex Selected Pdf Sgwid 0 0 45 P

Vectors And The Geometry Of Space Monografias Com

Nikon Z7 Ii Review

Manual De Ejercicios Resueltos De Quimica Analitica Cuantitativa

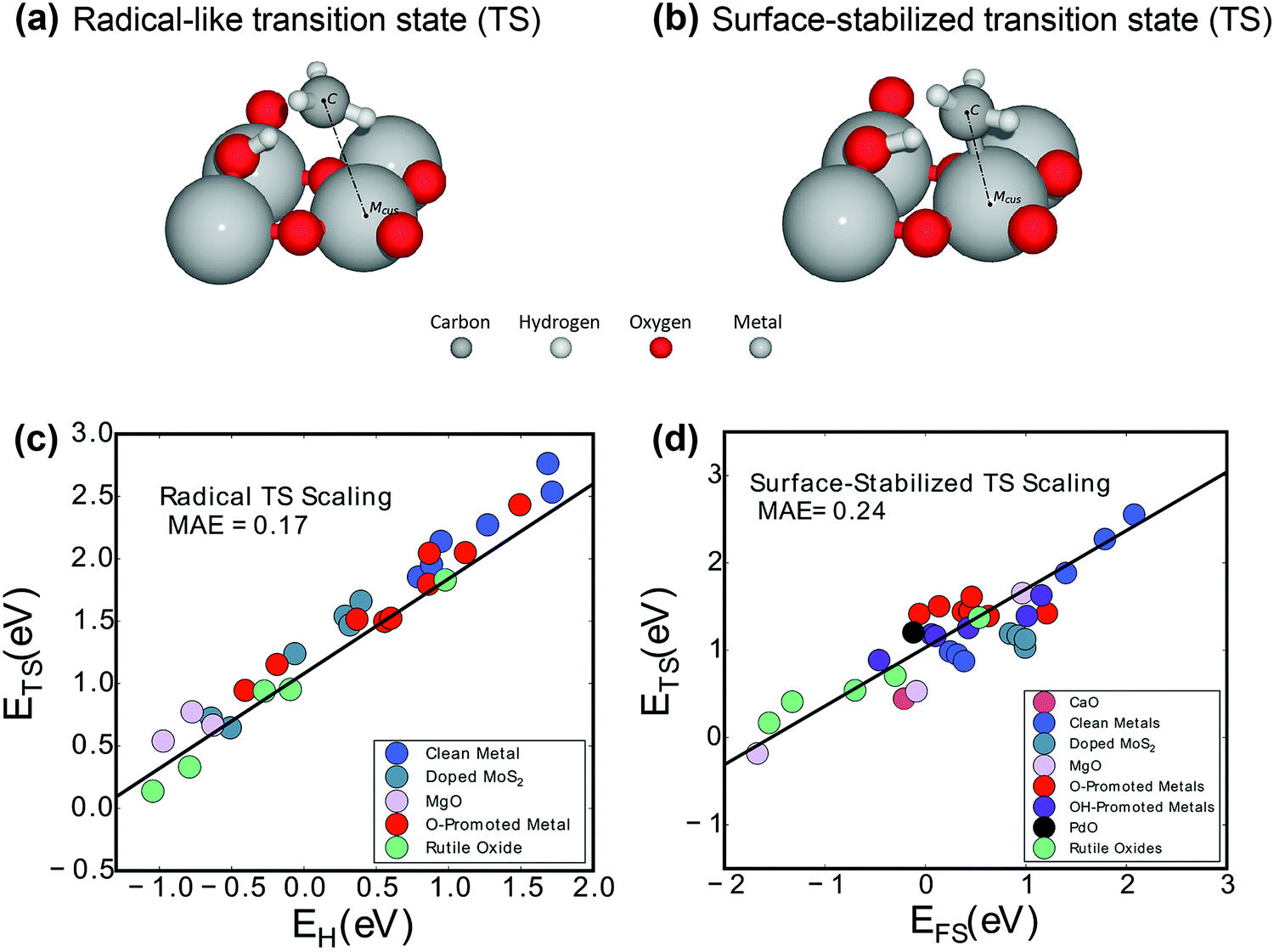
C H Bond Activation In Light Alkanes A Theoretical Perspective Chemical Society Reviews Rsc Publishing Doi 10 1039 D0csa

Http Www Econ Yale Edu Smith Econ510a Notes99 Pdf

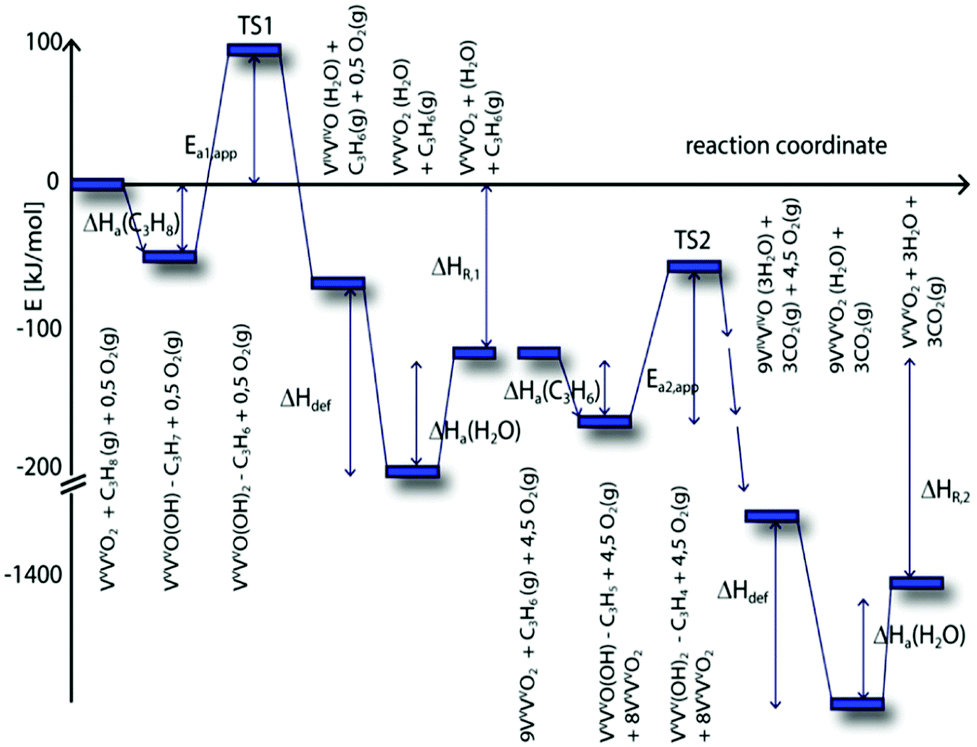
C H Bond Activation In Light Alkanes A Theoretical Perspective Chemical Society Reviews Rsc Publishing Doi 10 1039 D0csa

Nnu Net A Self Configuring Method For Deep Learning Based Biomedical Image Segmentation Nature Methods

Http Www Math Jhu Edu Gradexam Analysisexams Pdf

List Of Unicode Characters Wikipedia

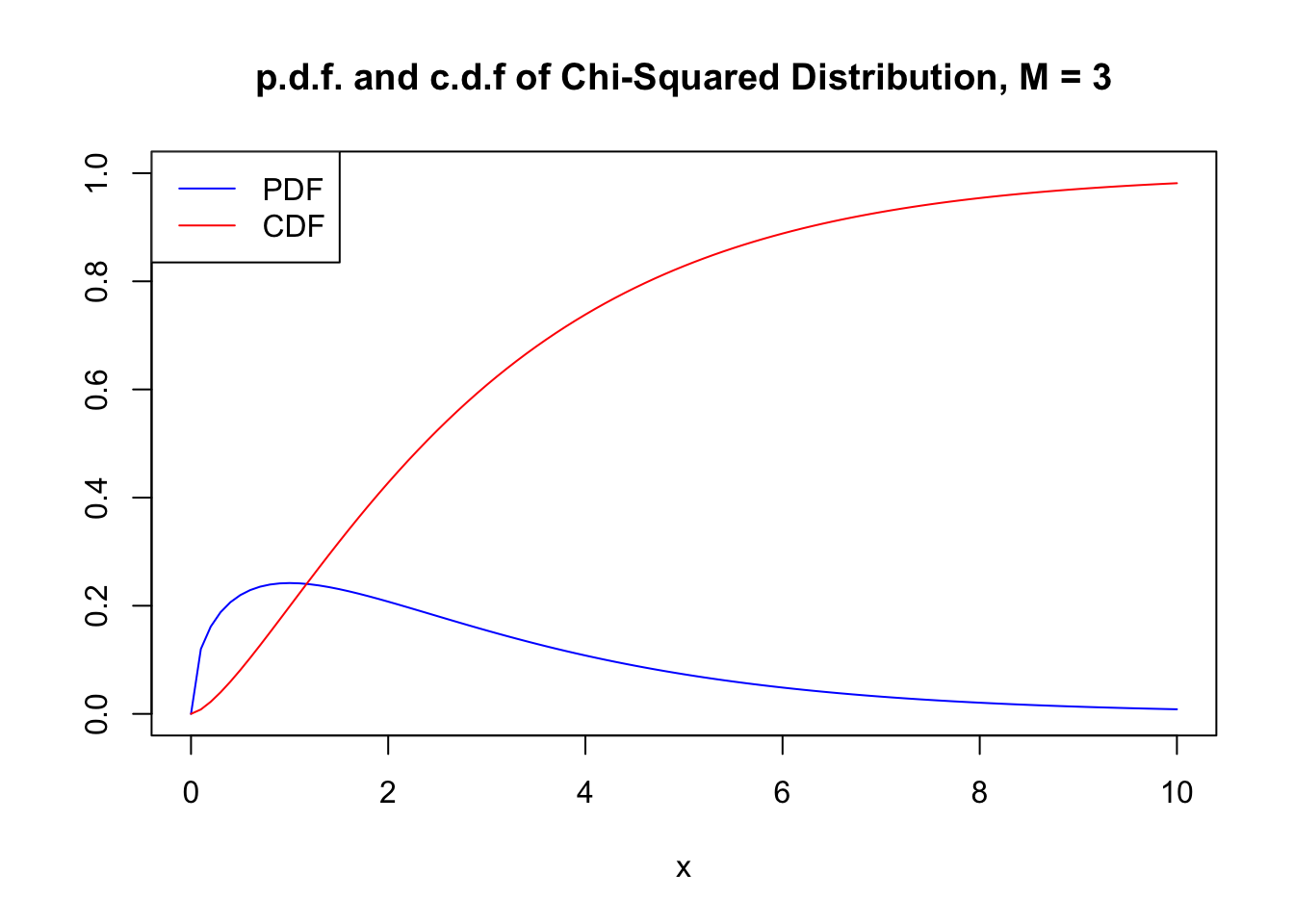
2 1 Random Variables And Probability Distributions Introduction To Econometrics With R

Determination Of Strong Phase Parameters In D K S L 0 Pi Pi

Vectors And The Geometry Of Space Monografias Com

Www Festo Com Cat En Gb Gb Data Doc Engb Pdf En Ms Config Combination En Pdf

Observation Of Psi 3686 P P Over Bar Eta And Improved Measurement Of J Psi P P Over Bar Eta

Libro 1er Ano De Bachillerato Esmate By Ufg Issuu

8 Ejercicios De Polinomios 2 Eso Parte 1 Superprof

Remote Sensing Free Full Text Precise And Robust Ship Detection For High Resolution Sar Imagery Based On Hr Sdnet Html

2º Algebra

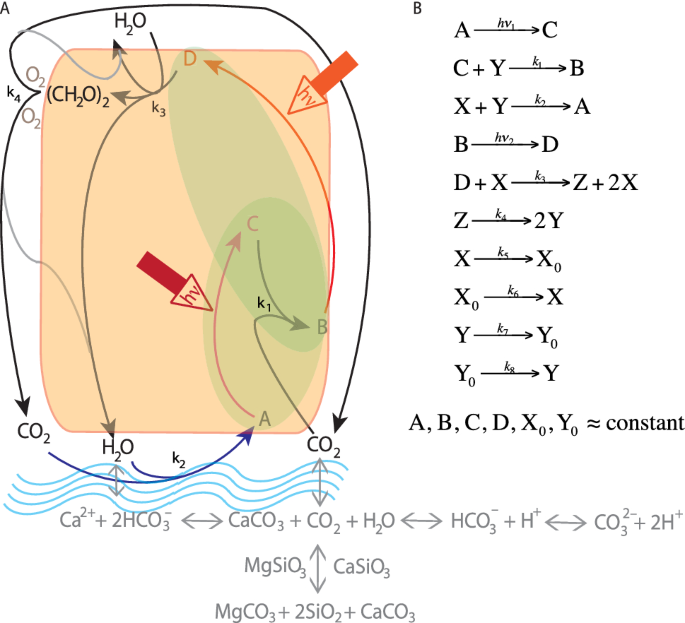
Self Sustained Oscillations And Global Climate Changes Scientific Reports

Mcrkpx9d6ltghm

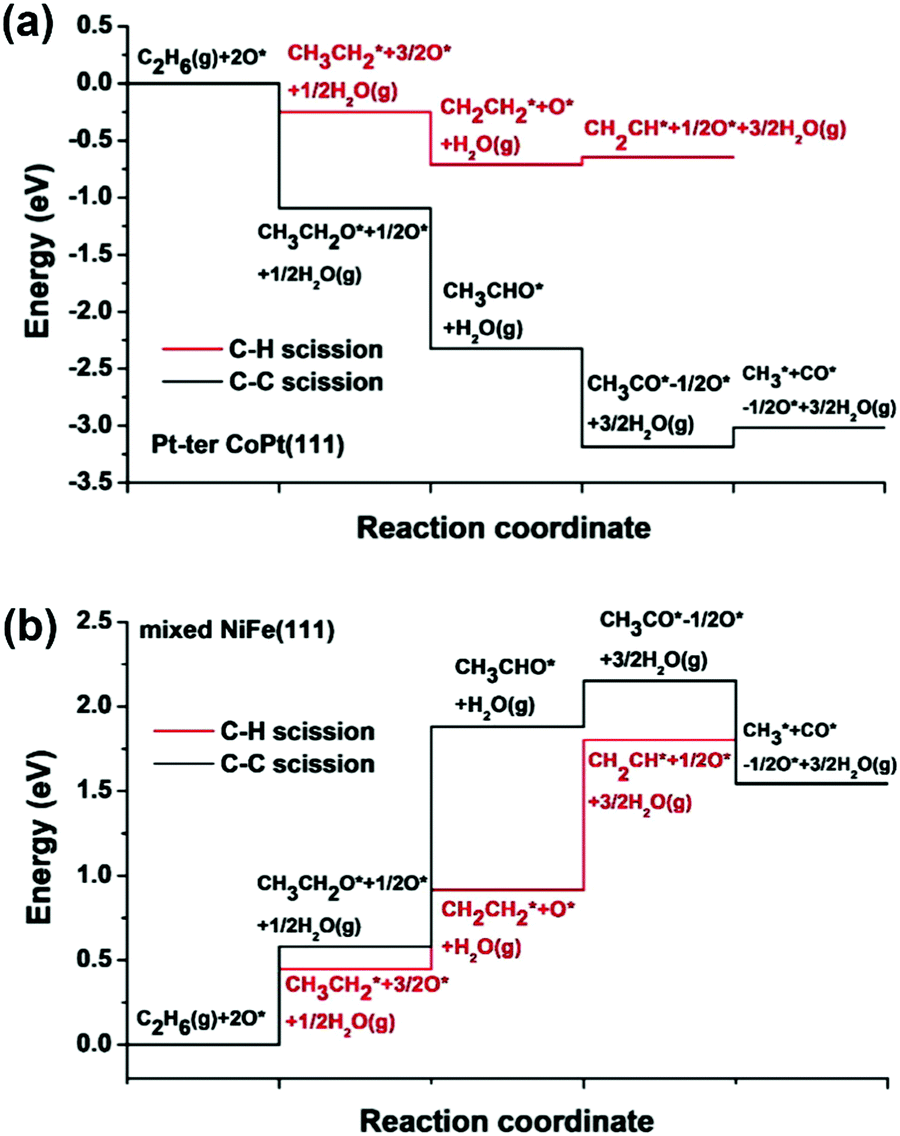
C H Bond Activation In Light Alkanes A Theoretical Perspective Chemical Society Reviews Rsc Publishing Doi 10 1039 D0csa

Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1

Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf

Wbjee 17 Maths Solved Question Paper Download Pdf

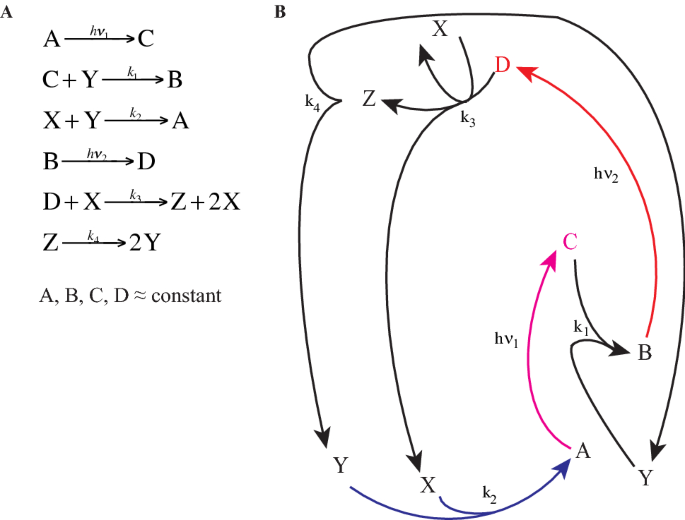
Self Sustained Oscillations And Global Climate Changes Scientific Reports

Www Springer Com Cda Content Document Cda Downloaddocument Sol Manual Complex Selected Pdf Sgwid 0 0 45 P

2

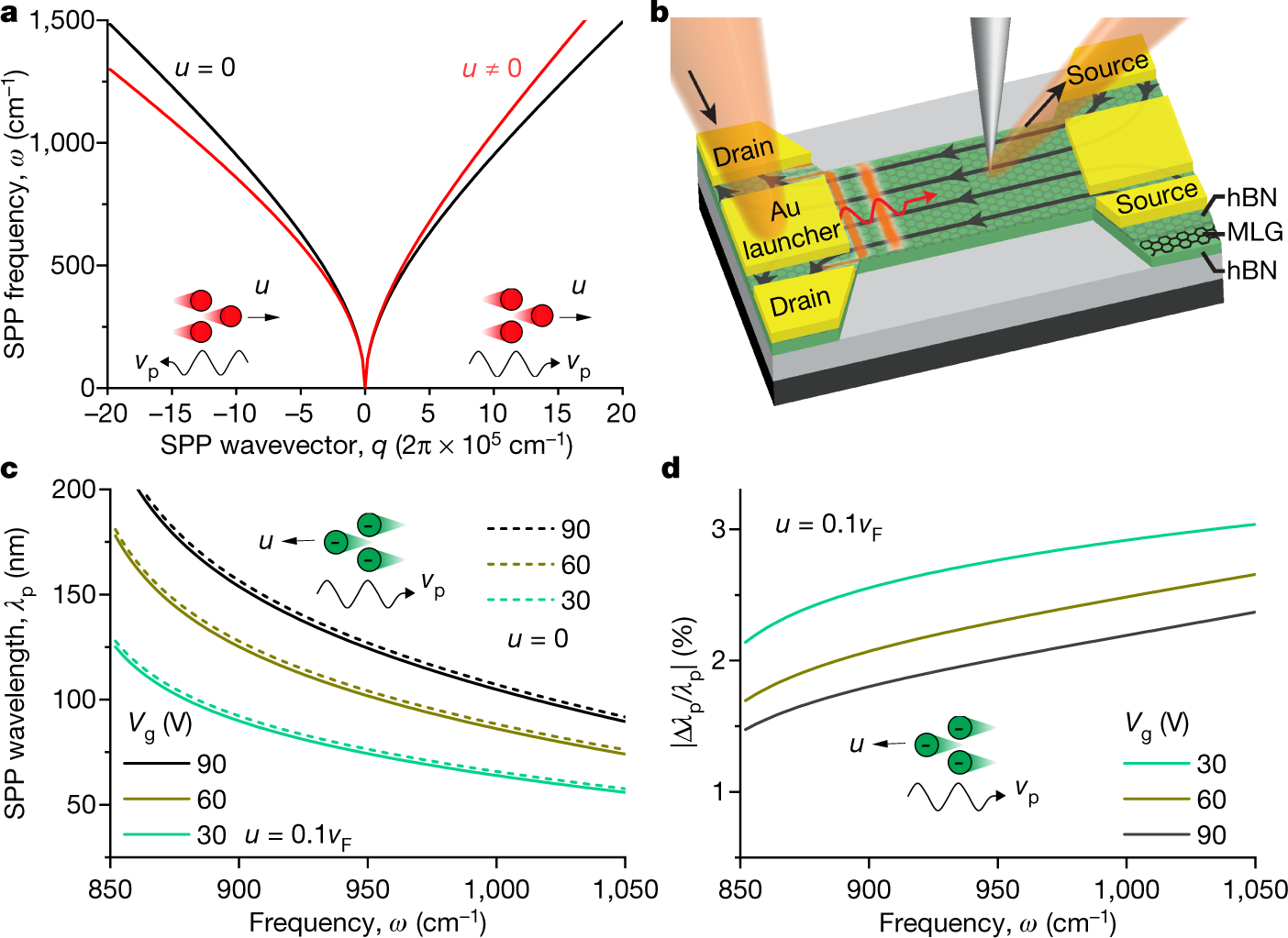
Wewmtijsi2tecm

A J V Curves B C V And Dlcp Measurements Of Cm X Z 1ax Tsse Download Scientific Diagram

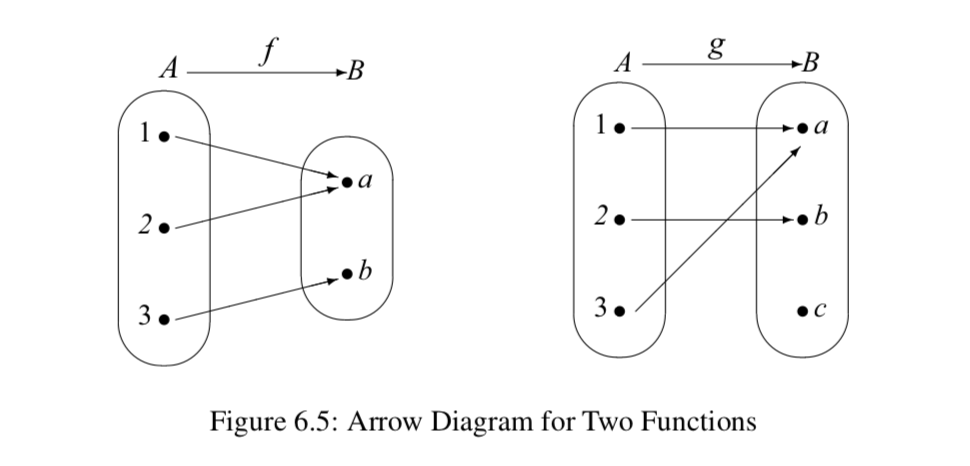
6 3 Injections Surjections And Bijections Mathematics Libretexts

Arxiv Org Pdf 1812

Www Festo Com Cat En Gb Gb Data Doc Engb Pdf En Ms Config Combination En Pdf

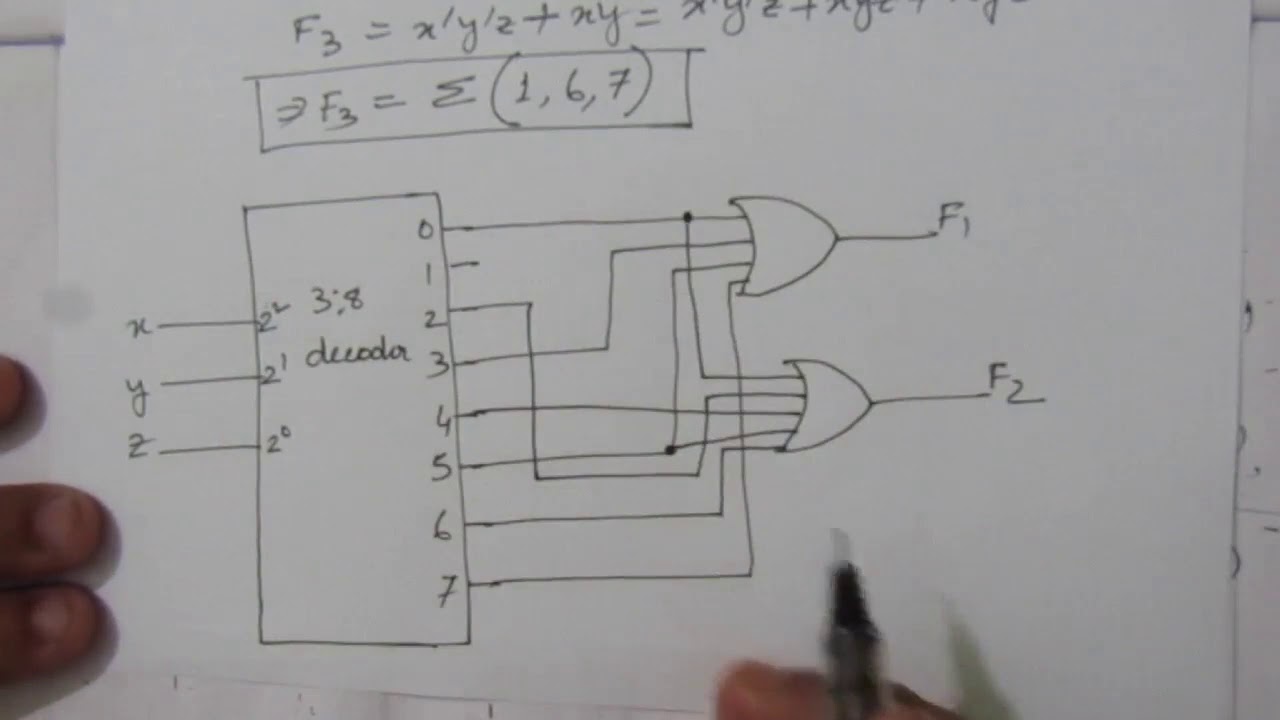
Q 4 30 Using A Decoder And External Gates Design The Combinational Circui Defined By The Followin Youtube

Ejercicios De La Ecuacion De La Recta Tangente Y Normal

Www Theglobalfund Org Media 3177 Bm14 10trpround6 Report Ar Pdf

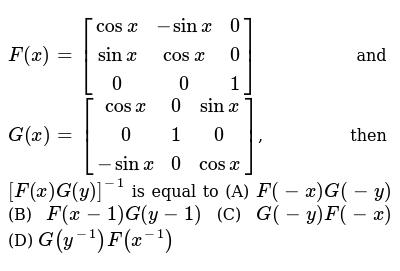
F X Cosx Sinx 0 Sinx Cosx 0 0 0 1 And G X Cosx 0 S

Www Math Utah Edu Wortman 1050 Text If Pdf

Link Aps Org Pdf 10 1103 Physrevd 101

Altgr Key Wikipedia

Vectors And The Geometry Of Space Monografias Com

A Review Of Boron Carbon Nitride Thin Films And Progress In Nanomaterials Sciencedirect

Vectors And The Geometry Of Space Monografias Com

If A B C Are Matrices Such That A X Y Z B A H G H B

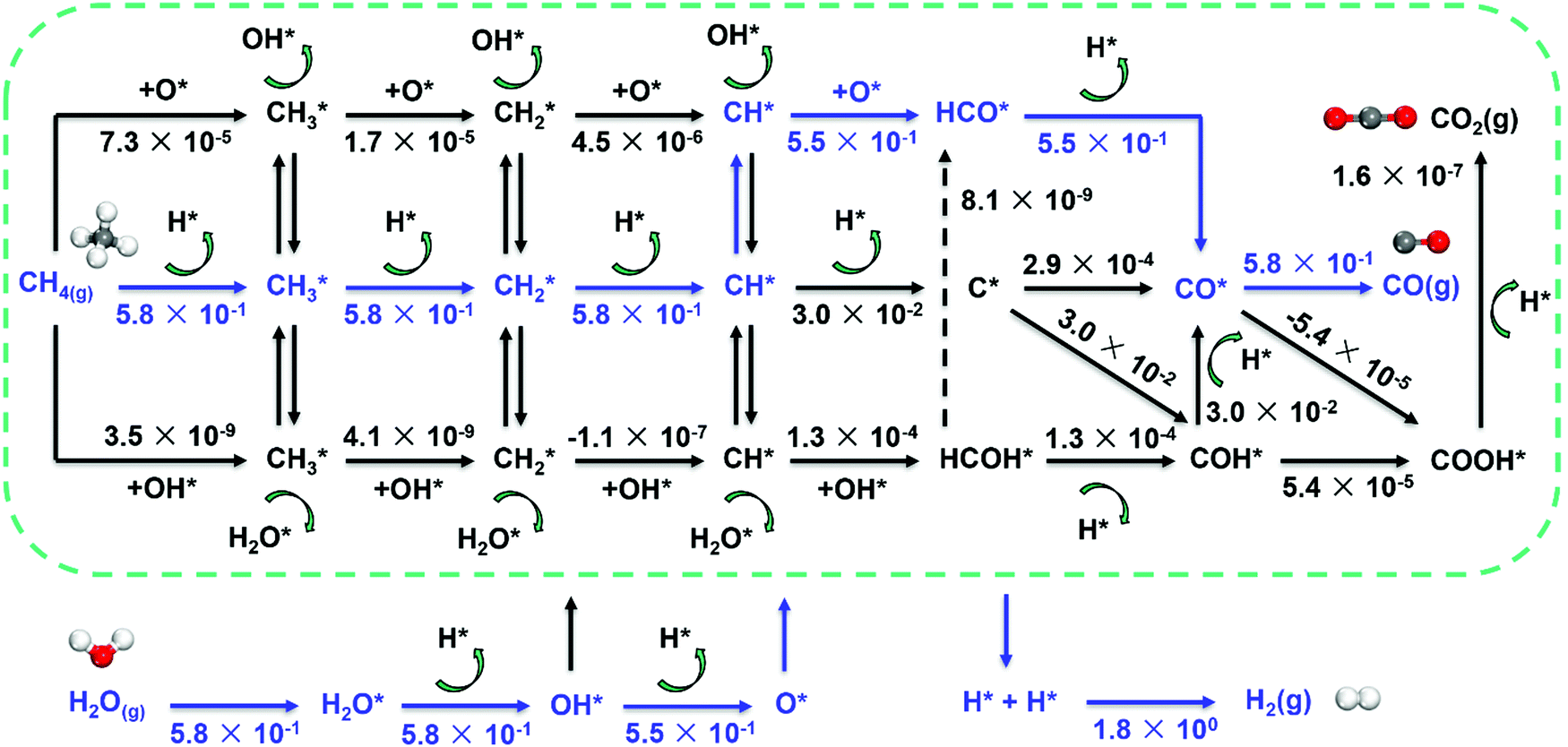
C H Bond Activation In Light Alkanes A Theoretical Perspective Chemical Society Reviews Rsc Publishing Doi 10 1039 D0csa

Pdf On The Sylvester Equation Ax Xb C

Vectors And The Geometry Of Space Monografias Com

2